Biconnected Component (maximal set)
Biconnected Graph : 임의의 한 노드를 제거해도 나머지 모든 노드들이 연결되어 있는 그래프이다. 따라서 biconnected graph에는 cv가 존재하지 않는다 (무방향 그래프에서 정의되는 개념이다)
Biconnected Component : cv에 의해 끊어진 그래프들의 각 부분을 의미한다
BCC 내의 임의의 두 노드는 완전히 다른 (edge와 node가 겹치지 않는다) 2개 이상의 경로가 존재한다
cv가 있으면, 그래프 전체가 BCC가 아니다(정의와 모순됨)
기본적으로 cycle을 BCC라고 한다
cv가 있었는데, 사라지면 연결이 끊기는 것이므로 BCC상태가 아니다
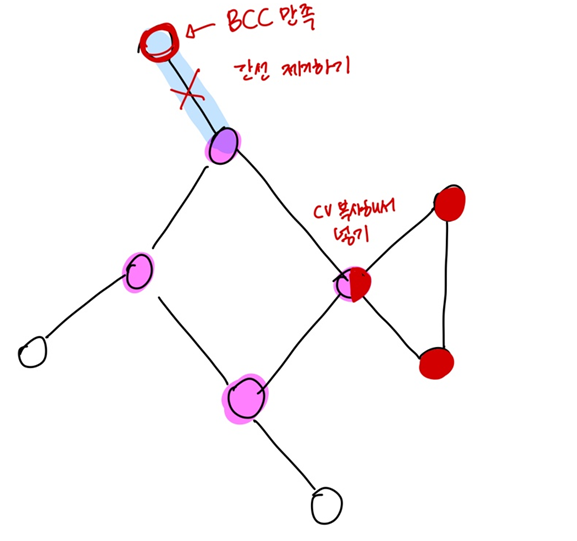
* cv는 여러 BCC에 걸쳐있다
* cv가 아닌 노드는 하나의 BCC에만 포함된다
위 그림처럼 cv를 먼저 찾고 간선을 포함하지 않거나(하나의 정점은 BCC이다) cv를 복사해서 넣는다
*단 간선을 제거하는 경우는 O-O일 경우! //다른 경우도 있나...? cv가 두개일때인가
#즉, cv를 찾고 BCC를 찾는다
그럼 cv를 어떻게 찾을 수 있을까?
DFS를 하고 cv에서 멈추면 안된다
위 그림처럼 BCC개수가 5개임에도, 하나의 cv를 찾으면 다음으로 못넘어가기 때문
cv알고리즘에서 각 서브트리는 BCC로 만들어질 수 있다

위 그림처럼 세개를 따로 푼다 ///!!
왜 같은 문제인가? 나눠진 각 서브트리의 자식들 노드끼리 묶어지는 BCC가 나올 확률이 없기 때문이다
노드개수가 줄었으므로 재귀로 풀면된다
1) 자식 노드들의 back edge가 루트노드(cv)를 넘어설 때(올라올때) 사이클이 되므로, 루트가 BCC에 들어있다는 것을 알 수 있다
2) 자식 노드들의 back edge가 루트노드(cv) 아래일 때, (루트를 포함 X)자식 노드들(서브트리)에 대해 DFS를 하고 BCC를 찾는다
Topological Sort
: 모든 edge가 왼쪽에서 오른쪽으로 가도록 한줄로 sorting하는 것
DAG : Directed Acyclic Graph (단방향 사이클이 없는 그래프)
사이클이 있으면 TS가 불가능하다
왜? 앞으로 연결된 edge를 타고 들어올 것이기 때문이다
사이클이 없으면 항상 TS가 가능하다 - 알고리즘에 의해 증명이 가능하다
Observation
step1)
indegree(들어오는 edge개수)가 0인 노드가 하나라도 있어야한다
indegree가 0인 노드가 없다면, 사이클이 되기 때문이다(노드를 따라 들어가는 과정이 멈출 수 없다)
=사이클이 없다면, indegree가 0인 노드가 있다
무작정 노드를 단방향으로 쭉 나열한다면
순서대로 쭉 나열했을 때 원래그래프 edge를 넣어도 된다는 증명이 필요하다
Indegree가 0인 노드를 앞에 세운다
뒤는 TS를 놓는다
TS가 된 노드들 중 Indegree가 0인 노드로 가는 edge가 없다 = indegree가 0이기 때문
노드 하나를 빼도 DAG이다 (=재귀할 수 있다)
왜? DAG가 아니라면 사이클이 있어야한다. 노드 하나를 뺐는데 사이클이 있다는 것은 그 전부터 사이클이 있었다는 뜻과 같다. 사이클이 없었는데(TS) 있어졌다? 즉, 이 말은 모순이 된다
DAG에서 indegree가 0인 노드를 하나씩 지운다 = DFS 후 n에 대해 수행하므로
=> O(mn)
step2)
더 빠르게 할 수는 없을까? 이벤트 큐를 사용하면 된다
DFS로 indegree를 계산하고 indegree가 0인 것을 큐에 넣는다
해당 노드를 뽑을 때 indegree가 바뀌는 노드들을 본다
indegree가 0인 노드들이 새로 생기면 이벤트가 되고, 큐에 넣는다
step3)
DFS를 하고 Post Numbers를 계산한다
Post Numbers(DFS가 리턴되는 순서)가 감소하는 순으로 나열한다

위 그림에서(위 그래프는 DAG이다) DFS가 a에서 시작하는 경우(a에서 b로 가는게 있다면 사이클이 만들어지므로 X)
Post Number는 1 그다음 b를 보기 때문에 b의 Post Number는 2이다
DFS가 b에서 시작하는 경우 a와 연결되어 있으므로 a가 1, b가 2이다
즉, b>a는 항상 만족하게 된다(Free Numbers는 항상 만족하진 않음)
따라서 Post Numbers(DFS가 리턴되는 순서)가 감소하는 순으로 나열하면 된다
DAG의 Shortest and Longest Path
Shortest Path(min) : 다익스트라
Longest Path(max) : NP-Complete
원래 다익스트라 간선이 음수이면 안되지만, DAG로 하면 음수가 있어도 가장 짧은 경로를 찾을 수 있다
//왜 가능하지?
DP 동전 거스름돈과 유사하다
보내는 식 or 당기는 식 둘 중 하나로 보면 된다
시간복잡도 : O(m+n)
The Shortest path in a DAG
src(indegree=0) => dest(outdegree=0)
//앞과 차이점은?
The Longest path in a DAG
가장 오래 걸리는 길 = 이 기을 줄이면 전체 process의 길이가 줄어든다
'Algorithm > Basic Concept' 카테고리의 다른 글
| [Lecture] SCC (0) | 2024.02.14 |
|---|---|
| [Lecture] Cut Vertex (0) | 2024.02.14 |
| [Lecture] Graph Traversal (0) | 2024.02.14 |
| [Lecture] Greedy Algorithms, Minimum Spanning Tree (0) | 2023.09.14 |
| [Lecture] Sum, Binary Search, Selection Sort (0) | 2023.09.12 |

